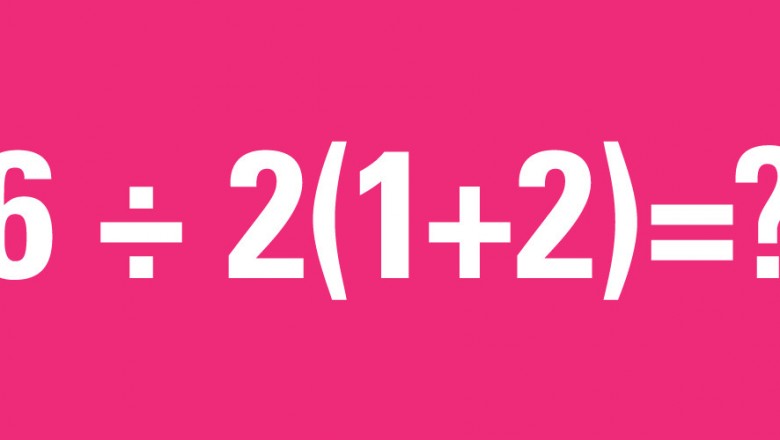
wyświetlenia

Zagadki matematyczne często wydają się proste. To znaczy do momentu w którym zaczniemy je rozwiązywać i nagle okazuje się, że nie mamy pojęcia co robimy. Często zdarza się też, że wpadamy na rozwiązanie w przeciągu kilku sekund, niestety po sprawdzeniu, odpowiedź okazuje się być zupełnie inna. Z powodu swojej zwodniczej łatwości, zagadki matematyczne są niesamowicie popularne w internecie.
Oto niektóre z nich:
1. Jaką cyfrę powinno się wstawić w miejsce znaku zapytania?
Zacznijmy od czegoś banalnego. Czy wpadniesz na to jaka cyfra powinna znaleźć się w miejscu oznaczonym znakiem zapytania?

Odpowiedź: 6.
Wyjaśnienie: Suma cyfr we wszystkich wierszach i kolumnach powinna wynosić 15.
2. Kij i piłka.
Kij i piłka do bejsbolu kosztują razem jednego dolara i dziesięć centów. Kij kosztuje dolara więcej niż piłka. Ile wynosi koszt piłki?

Jeżeli twoja odpowiedź wynosi 10 centów, mylisz się.
Odpowiedź: Piłka kosztuje 5 centów.
Wyjaśnienie: Czytając zagadkę zapewne uznałeś, że skoro kij i piłka kosztują razem dolara i dziesięć centów, a sam kij kosztuje dolara więcej niż piłka, odpowiedź 10 centów wydaje się oczywista bez żadnych obliczeń.
Gdy jednak poświęcisz chwilę na obliczenia, szybko uzmysłowisz sobie, że różnica między $1 a 10 centami wynosi 90 centów, a nie 1$. Jedyną możliwością aby kij był droższy od piłki o dolara, a zarazem ich łączny koszt wynosił $1.10 jest: cena kija wynosząca $1.05 i cena piłki wynosząca 5 centów.
3. Zmienić czy nie zmienić.
Wyobraź sobie, że bierzesz udział w teleturnieju, i masz do wyboru 3 drzwi. Za jednymi z nich kryje się milion dolarów, za pozostałymi nie ma nic. Wybierasz drzwi #1, a prowadzący, który wie co kryje się za każdymi z drzwi, otwiera inne z nich, powiedzmy #3, za którymi nie ma nic. Następnie prowadzący zadaje ci pytanie: Zostajesz przy wybranych drzwiach, czy może chcesz zmienić decyzję?

A więc co jest lepszym wyborem, zostanie przy wybranych drzwiach, czy zmiana?
Większość ludzi uzna zapewne, że wybór nie ma znaczenia, bo przecież i tak nasze szanse na nagrodę wynoszą 50/50. Jest to jednak nieprawda.
Odpowiedź: Zawsze powinno się zmienić drzwi.
Wyjaśnienie: Gdy na początku wybrałeś jedne z trzech drzwi, twoje szanse na nagrodę wynosiły 1 do 3, a co za tym idzie, ryzyko wybrania pustych drzwi wynosiło 2 do 3. Błędem jest jednak założenie, że skoro zostało tylko dwoje drzwi, mamy 50% szansy, że nasz pierwotny wybór był trafny. W rzeczywistości, nasze szanse nie uległy zmianie.
Prawdopodobieństwo prawidłowych drzwi wciąż wynosi 1 do 3, a nieprawidłowych 2 do 3, co znaczy, że gdy prowadzący otworzył jedne z pustych drzwi, wyeliminował on jeden z BŁĘDNYCH wyborów, a szanse na to, że nagroda znajduje się za ostatnimi zamkniętymi drzwiami wciąż wynosi 2 do 3 – dwa razy więcej niż przy naszym oryginalnym wyborze. Krótko mówiąc, zamieniając drzwi, masz 2 do 3 szansy, że twój pierwszy wybór był zły.
Pewnie, nie ma gwarancji, że zamieniając drzwi wygramy, ale statystycznie, grając raz za razem, 2 na 3 razy dzięki tej metodzie zdobędziemy nagrodę.
Wciąż nie wiesz o co chodzi? Za pomocą kilku diagramów wyjaśni ci to profesor matematyki z uniwersytetu UC Berkeley, Lisa Goldberg.
4. Proste działanie
Jakie wyszło ci rozwiązanie tego pozornie banalnego działania?

Ta zagadka dzieli całe rzesze ludzi. Niektórzy są ABSOLUTNIE pewni, że odpowiedzią jest 1, inni są przekonani, że prawidłowa odpowiedź to 9.
Odpowiedź: Rację mają ci drudzy, prawidłowa odpowiedź to 9.
Wyjaśnienie: Już dzieci w podstawówce uczy się kolejności wykonywania działań. W pierwszej kolejności wykonujemy działania w nawiasach. Nasze działanie przedstawia się wtedy w następujący sposób: 6/2(3)=? Wiele osób uważa, że kolejnym krokiem powinno być pomnożenie dwójki z trójką znajdującą się w nawiasie. Reguła kolejności wykonywania działań mówi jednak jasno: Po rozwiązaniu działań w nawiasach wykonujemy mnożenie lub dzielenie W KOLEJNOŚCI OD LEWEJ STRONY. Błędem jest więc następujące rozwiązanie: 6/2*(3) = 6/6 = 1
Prawidłowym zapisem jest oczywiście: 6/2*(3) = 3*(3) = 9
5. Zagadka z liliami.
W pewnej wiosce znajduje się staw porośnięty liliami. Z każdym dniem lilie rozrastają się podwajając swój rozmiar. Po 48 dniach cały staw jest porośnięty liliami. Ile zatem dni potrzeba było aby lilie przykryły połowę stawu?

Kusząca wydaje się odpowiedź: 24 – ale jest ona fałszywa.
Odpowiedź: Lilie przykryją połowę stawu w 47 dni.
Wyjaśnienie: W zadaniu jest wyraźnie podane, że lilie podwajają swój rozmiar każdego dnia, co znaczy, że każdego dnia ich rozmiar zwiększał się dokładnie o połowę. Skoro więc wiemy, że lilie pokryją cały staw w przeciągu 48 dni, oczywiste jest, że w dniu 47 ich rozmiar był o połowę mniejszy, czyli zakrywał połowę stawu.
Daliście radę ze wszystkimi ? Podzielcie się ze znajomymi i sprawdźcie ich !




















Rozmowy na Facebooku